
Stoichiometry is simply the math behind chemistry. Given enough information, one can use stoichiometry to calculate masses, moles, and percents within a chemical equation.

A mole simply represents Avogadro's number (6.022 x 1023) of molecules. A mole is similar to a term like a dozen. If you have a dozen carrots, you have twelve of them. Similarly, if you have a mole of carrots, you have 6.022 x 1023 carrots. In the equation above there are no numbers in front of the terms, so each coefficient is assumed to be one (1). Thus, you have the same number of moles of AgNO3, NaCl, AgCl, NaNO3.
Converting between moles and grams of a substance is often important. This conversion can be easily done when the atomic and/or molecular mass of the substance(s) are known. Given the atomic or molecular mass of a substance, that mass in grams makes a mole of the substance. For example, calcium has an atomic mass of 40 atomic mass units. So, 40 grams of calcium makes one mole, 80 grams makes two moles, etc.
Example
Molar Mass of Ca = 40.08 (From the Periodic Table)
How many moles of Ca are in 4.50 grams of Ca?

Sometimes when reactions occur between two or more substances, one reactant runs out before the other. That is called the "limiting reagent". Often, it is necessary to identify the limiting reagent in a problem.
Example: A chemist only has 6.0 grams of C2H2 and an unlimited supply of oxygen and he desires to produce as much CO2 as possible. If she uses the equation below, how much oxygen should she add to the reaction?
To solve this problem, it is necessary to determine how much oxygen should be added if all of the reactants were used up (this is the way to produce the maximum amount of CO2)./p>
First, we calculate the number of moles of C2H2 in 6.0 g of C2H2. To be able to calculate the moles we need to look at a periodic table and see that 1 mole of C weighs 12.0 g and H weighs 1.0 g. Therefore we know that 1 mole of C2H2 weighs 26 g (2 × 12 grams + 2 × 1 gram).
| 6.0 g C2H2 x |
(24.0 + 2.0)g C2H2 |
= 0.25 mol C2H2 |
Then, because there are five (5) molecules of oxygen to every two (2) molecules of C2H2, we need to multiply the result by 5/2 to get the total molecules of oxygen. Then we convert to grams to find the amount of oxygen that needs to be added:
|
0.25 mol C2H2 x |
2 mol C2H2 |
x |
1 mol O2 |
= 20 g O2 |
We can consider percent by mass (or weight percent, as it is sometimes called) in two ways:
We need two pieces of information to calculate the percent by mass of a solute in a solution:
Use the following equation to calculate percent by mass:

Molarity tells us the number of moles of solute in exactly one liter of a solution. (Note that molarity is spelled with an "r" and is represented by a capital M.)
We need two pieces of information to calculate the molarity of a solute in a solution:
To calculate molarity we use the equation:

Writing Expressions for Kc
The general equilibrium expression for a reaction:
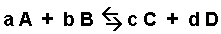
is written as:
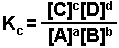
The brackets "[ ]" represent the concentration of the species (moles per liter or molarity). "a, b, c, and d" represent the coefficients used to balance the equation. The "c" in Kc indicates that the value of K is determined using the concentrations of each species.
There are two cases when a species is not shown in the equilibrium expression:
Writing Expressions for Kp
When one or more of the species in a system exists in the gaseous phase, the partial pressure of that species can be used in the equilibrium expression Dissolved species are still expressed as moles per liter (molarity).
Examples
Examples of equilibrium expressions Kc for a variety of equilibrium systems follow. When one or more gaseous substances are involved, the Kp expression is also given.






In making an ICE chart the following items should be noted:
The following is a "how to" make an ICE chart using the example to illustrate the process.
Example: A mixture consisting initially of 3.00 moles NH3, 2.00 moles of N2, and 5.00 moles of H2, in a 5.00 L container was heated to 900 K, and allowed to reach equilibrium. Determine the equilibrium concentration for each species present in the equilibrium mixture.
2 NH3(g) ![]() N2(g) + 3 H2(g) Kc = 0.0076 @ 900 K
N2(g) + 3 H2(g) Kc = 0.0076 @ 900 K

|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) | |||
| Equilibrium Conc. (M) |

|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) |
|
|
|
| Equilibrium Conc. (M) |
|
|
|
|
|
| Initial Concentration (M) |
|
|
|
| Change in Conc. (M) |
|
|
|
| Equilibrium Conc. (M) |
|
|
|

The value of x was determined using the method of successive approximations.
Determining the Average Rate from Change in Concentration over a Time Period
We calculate the average rate of a reaction over a time interval by dividing the change in concentration over that time period by the time interval. For the change in concentration of a reactant, the equation, where the brackets mean "concentration of", is

Note: We use the minus sign before the ratio in the previous equation because a rate is a positive number. We do not need the minus sign when calculating average rates from products.

Determining the Instantaneous Rate from a Plot of Concentration Versus Time
An instantaneous rate is the rate at some instant in time. An instantaneous rate is a differential rate: -d[reactant]/dt or d[product]/dt.
We determine an instantaneous rate at time t:

Determining the Initial Rate from a Plot of Concentration Versus Time
The initial rate of a reaction is the instantaneous rate at the start of the reaction (i.e., when t = 0). The initial rate is equal to the negative of the slope of the curve of reactant concentration versus time at t = 0.
If we run an exothermic reaction in solution in a calorimeter, the heat produced by the reaction is trapped in the calorimeter and increases the temperature of the solution. If we run an endothermic reaction, the heat required by the reaction is removed from the solution and the temperature of the solution decreases.

We can calculate the amount of heat absorbed by the solution or the amount of heat removed from the solution with the following equation:

Note:
